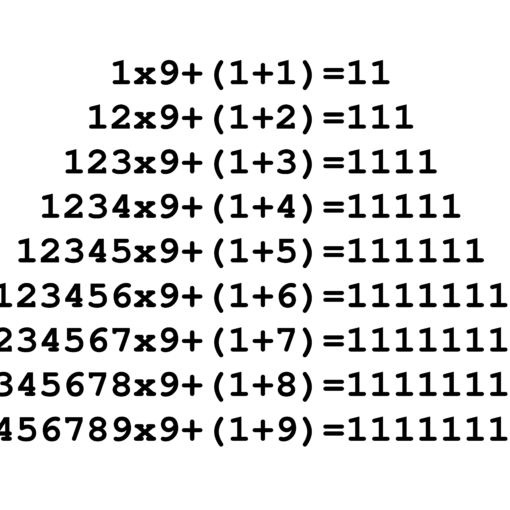Piramide numerica, numeri repunit e numeri dalle cifre consecutive

Un numero naturale n viene generalmente rappresentato in una base numerica q associando una “sequenza finita di numeri naturali” $n_k n_{k-1} n_{k-2} .... n_2 n_1 n_0$ , ciascuno scelto tra 0 e q-1, in modo tale che valga l’uguaglianza $n={n_kq^k}+n_{k-1} q^{k-1}+n_{k-2} q^{k-2}+....+n_2 q^2+n_1 q^1+n_0$
In questa trattazione ci interesseranno i numeri naturali in cui la “sequenza finita di numeri naturali” è formata da numeri naturali consecutivi $1234..(n-2)(n-1)n$ .
Chiameremo questi numeri con il termine generico $S_n$ e la rispettiva somma della serie numerica con base q assumerà la forma:

$\textcolor{black}{\displaystyle\sum_{k=1}^n kq^{n-k}}$ 1.1

riscriviamo la serie in forma estesa:

$\textcolor{black}{S_n=1 q^{n-1}+2q^{n-2}+3q^{n-3}+ ....}$
$\textcolor{black}{....+(n-2)q^2+(n-1)q^1+n}$ 1.2

moltiplichiamo la 1.2 membro a membro per il fattore q

$\textcolor{black}{S_nq=1q^n+2q^{n-1}+3q^{n-2}+....}$
$\textcolor{black}{....+(n-2)q^3+(n-1)q^2+nq}$ 1.3

sottraiamo membro a membro alla 1.3 la 1.2 e raccogliamo a fattore comune al secondo membro i monomi simili

$\textcolor{black}{S_nq-S_n=1q^n+(2-1)q^{n-1}+(3-2)q^{n-2}+....}$
$\textcolor{black}{....+(n-2-n+3)q^3+(n-1-n+2)q^2+(n-n+1)q-n}$

possiamo notare che i termini all’interno delle parentesi rotonde al secondo membro valgono tutti 1, otteniamo quindi:

\textcolor{black}{S_n q-S_n=\displaystyle\sum_{k=1}^n q^{n-k+1}-n}

ovvero:

$\textcolor{black}{S_n q-S_n=q\displaystyle\sum_{k=1}^n q^{n-k}-n}$ 1.4

spostiamo il termine “n” al primo membro

$\textcolor{black}{S_n q-S_n+n=q\displaystyle\sum_{k=1}^n q^{n-k}}$ 1.5

ed esplicitiamola con le sommatorie della 1.1

\textcolor{black}{(q-1)\displaystyle\sum_{k=1}^n kq^{n-k}+n=q\displaystyle\sum_{k=1}^n q^{n-k}=\displaystyle\sum_{k=1}^n q^{k}}

Aggiungiamo l’unità ad ambo i membri

\textcolor{black}{(q-1)\displaystyle\sum_{k=1}^n kq^{n-k}+n+1=\displaystyle\sum_{k=0}^n q^{k}}

esplicitiamo l’uguagliana per il primo termine del primo membro e otteniamo:

$\textcolor{black}{(q-1)\displaystyle\sum_{k=1}^n kq^{n-k}=\displaystyle\sum_{k=0}^n q^{k}-(n+1)}$ 1.6

Sottraiamo $S_n$ alla 1.5 membro a membro

\textcolor{black}{S_n q-2S_n+n=q\displaystyle\sum_{k=1}^n q^{n-k}-S_n}

ed esplicitiamola con le sommatorie della 1.1

\textcolor{black}{q\displaystyle\sum_{k=1}^n kq^{n-k}-2\displaystyle\sum_{k=1}^n kq^{n-k}+n=q\displaystyle\sum_{k=1}^n q^{n-k}-\displaystyle\sum_{k=1}^n kq^{n-k}}

possiamo riscrivere la precedente nel modo compatto:

$\textcolor{black}{(q-2)\displaystyle\sum_{k=1}^n kq^{n-k}+n=\displaystyle\sum_{k=1}^n (q-k)q^{n-k}}$ 1.7

moltiplichiamo la 1.7 ambo i membri per (q-1)

\textcolor{black}{(q-2)(q-1)\displaystyle\sum_{k=1}^n kq^{n-k}+n(q-1)=\displaystyle (q-1)\sum_{k=1}^n (q-k)q^{n-k}}

e sostituiamo la 1.6 nella precedente

\textcolor{black}{(q-2)\displaystyle\sum_{k=0}^n q^{k}-(n+1)(q-2)+n(q-1)=\displaystyle (q-1)\sum_{k=1}^n (q-k)q^{n-k}}

con un po di algebra otteniamo:

\textcolor{black}{(q-2)\displaystyle\sum_{k=0}^n q^{k}+n=\displaystyle (q-2)+(q-1)\sum_{k=1}^n (q-k)q^{n-k}}

e scambiando i membri

$\textcolor{black}{\displaystyle (q-1)\sum_{k=1}^n (q-k)q^{n-k} + (q-2)=n+ (q-2)\displaystyle\sum_{k=0}^n q^{k}}$ 1.8

Se poniamo come base numerica q=10 e per “n” i rispettivi 9 valori: 1,2,3,4,5,6,7,8,9 nella 1.8, otteniamo le relazioni numeriche seguenti:

\textcolor{black}{\displaystyle 9\sum_{k=1}^n (10-k)10^{n-k} + 9=n+ 8\displaystyle\sum_{k=0}^n 10^{k}}

Per un altro esempio prendiamo la base numerica q=16 e per “n” i rispettivi 15 valori: 1,2,3,4,5,6,7,8,9,A,B,C,D,E,F dove per i numeri naturali >9 si sono presi come simboli le prime lettere dell’alfabeto, come si conviene per la base esadecimale. Dalla 1.8 otteniamo: