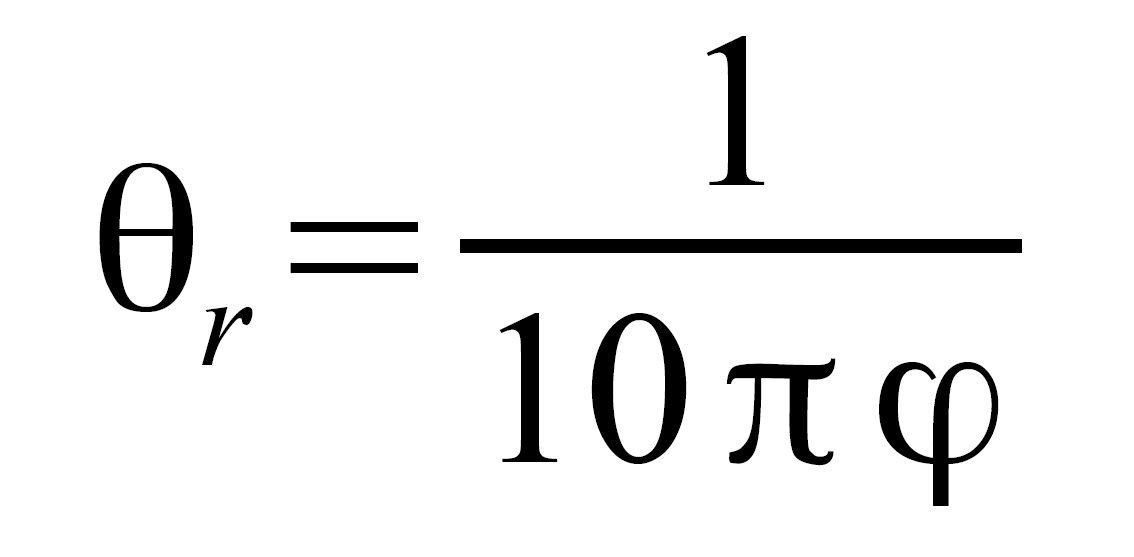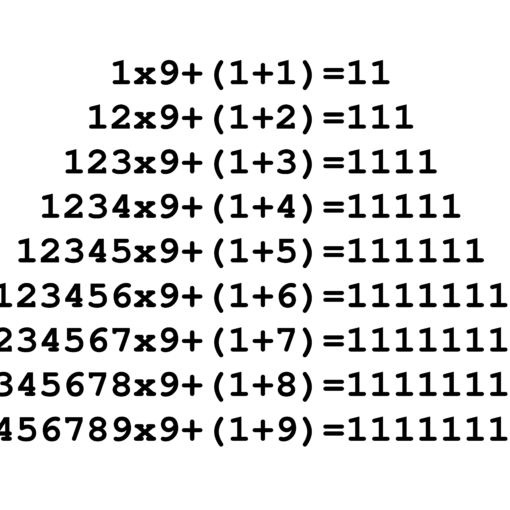Un numero naturale n viene generalmente rappresentato nel sistema posizionale con una base numerica q associando una “sequenza finita di numeri naturali” n_k n_{k-1} n_{k-2} .... n_2 n_1 n_0, ciascuno scelto tra 0 e q-1, in modo tale che valga l’uguaglianza n={n_kq^k}+n_{k-1} q^{k-1}+n_{k-2} q^{k-2}+....+n_2 q^2+n_1 q^1+n_0.
In questa trattazione ci interesseranno i numeri naturali palindromi con un numero dispari di cifre, in cui la “sequenza finita di numeri naturali” è formata da numeri naturali consecutivi simmetrici rispetto alla cifra centrale, 1234..(n-2)(n-1)n(n-1)(n-2)..4321.
Il primo “ramo ascendente” dei numeri palindromi 1234..(n-2)(n-1)n abbiamo già visto come ricavarlo, riportiamo il procedimento per comodità:
S_n^A=\displaystyle\sum_{k=1}^n kq^{n-k} 2.1
riscriviamo la serie in forma estesa:
S_n^A=1 q^{n-1}+2q^{n-2}+3q^{n-3}+ ....
....+(n-2)q^2+(n-1)q^1+n 2.2
moltiplichiamo la 2.2 membro a membro per il fattore q
{S_n^A}q=1q^n+2q^{n-1}+3q^{n-2}+....
....+(n-2)q^3+(n-1)q^2+nq 2.3
sottraiamo membro a membro alla 2.3 la 2.2 e raccogliamo a fattore comune al secondo membro i monomi simili
{S_n^A}q-{S_n}^A=1q^n+(2-1)q^{n-1}+(3-2)q^{n-2}+....
....+(n-2-n+3)q^3+(n-1-n+2)q^2+(n-n+1)q-n
possiamo notare che i termini all’interno delle parentesi rotonde al secondo membro valgono tutti 1, otteniamo quindi:
{S_n^A}q-S_n^A=\displaystyle\sum_{k=1}^n q^{n-k+1}-n
ovvero:
{S_n^A}q-S_n^A=q\displaystyle\sum_{k=1}^n q^{n-k}-n 2.4
esplicitando l’uguaglianza 2.4 rispetto a S_n^A otteniamo:
S_n^A={\frac 1 {q-1}} \lbrack{q\displaystyle\sum_{k=1}^n q^{n-k}-n}\rbrack
che si può scrivere :
S_n^A={\frac 1 {q-1}} \lbrack{q\displaystyle\sum_{k=1}^n q^{k-1}-n}\rbrack 2.5
Con lo stesso metodo ricaviamo il secondo “ramo discendente” dei numeri palindromi
n(n-1)(n-2)..4321:
S_n^D=\displaystyle\sum_{k=1}^n kq^{k-1} 2.6
riscriviamo la somma della serie in forma estesa:
S_n^D=1+2q^1+3q^2+4q^3+ ....
....+(n-2)q^{n-3}+(n-1)q^{n-2}+nq^{n-1} 2.7
moltiplichiamo la 2.7 membro a membro per il fattore q
S_n^Dq=1q^1+2q^2+3q^3+4q^4+ ....
....+(n-2)q^{n-2}+(n-1)q^{n-1}+nq^n 2.8
sottraiamo membro a membro alla 2.8 la 2.7 e raccogliamo a fattore comune al secondo membro i monomi simili
S_n^Dq-S_n^D=-1+(1-2)q^1+(2-3)q^2+(3-4)q^3+ ....
....+(n-2-n+1)q^{n-2}+(n-1-n)q^{n-1}+nq^n
possiamo notare che i termini all’interno delle parentesi rotonde al secondo membro valgono tutti -1, otteniamo quindi:
S_n^Dq-S_n^D=-\displaystyle\sum_{k=1}^n q^{k-1}+nq^n 2.9
esplicitando l’uguaglianza 2.9 rispetto ad S_n^D otteniamo:
S_n^D={\frac 1 {q-1}} \lbrack{{-\displaystyle\sum_{k=1}^n q^{k-1}+nq^n}\rbrack} 3.0
Dalla 3.0 ricaviamo S_{n-1}^D
S_{n-1}^D={\frac 1 {q-1}} \lbrack{{-\displaystyle\sum_{k=1}^{n-1} q^{k-1}+(n-1)q^{n-1}}\rbrack} , con facili passaggi
S_{n-1}^D={\frac 1 {q-1}} \lbrack{{-\displaystyle\sum_{k=1}^{n-1} q^{k-1}+nq^{n-1}-q^{n-1}}\rbrack}
il termine -q^{n-1} lo includiamo nella sommatoria e otteniamo:
S_{n-1}^D={\frac 1 {q-1}} \lbrack{{-\displaystyle\sum_{k=1}^n q^{k-1}+nq^{n-1}}\rbrack} 3.1
Per come è stata definita S_n^D nella 2.6 abbiamo che S_{n-1}^D+nq^{n-1}=S_n^D e per n=1 abbiamo S_0^D+1q^0=S_1^D=1q^0=1 e quindi S_0^D+1=1 e ci da S_0^D=0
Per ottenere il numero palindromo 1234..(n-2)(n-1)n(n-1)(n-2)..4321 occorre posizionare il ramo ascendente S_n^A in modo tale che la cifra meno significativa venga subito dopo la cifra più significativa del ramo discendente S_{n-1}^D , otterremo ciò moltiplicando S_n^A per q^{n-1}e sommandolo a S_{n-1}^D.
S_n^A q^{n-1}+S_{n-1}^D={\frac {q^{n-1}} {q-1}} \lbrack{q\displaystyle\sum_{k=1}^n q^{k-1}-n}\rbrack+{\frac 1 {q-1}} \lbrack{{-\displaystyle\sum_{k=1}^n q^{k-1}+nq^{n-1}}\rbrack}
Con un pò di algebra otteniamo:
S_n^A q^{n-1}+S_{n-1}^D={\frac 1 {q-1}} \lbrack{q^{n-1} q\displaystyle\sum_{k=1}^n q^{k-1}-\cancel{nq^{n-1}}}{{-\displaystyle\sum_{k=1}^n q^{k-1}+\cancel{nq^{n-1}}}\rbrack}
e in fine:
S_n^A q^{n-1}+S_{n-1}^D={\frac {q^n-1} {q-1}} \displaystyle\sum_{k=1}^n q^{k-1} 3.2
Considerando la somma della progressione geometrica , o numero repunit in base q: \sum_{k=1}^n q^{k-1} :
\sum_{k=1}^n q^{k-1}=q^{n-1}+q^{n-2}+q^{n-3}+....+q^2+q^1+1 3.3
La somma si ricava moltiplicando la 3.3 per q e sottraendo membro a membro la 3.3 stessa, otteniamo:
q\sum_{k=1}^n q^{k-1}-\sum_{k=1}^n q^{k-1}=q^{n-1}-1 ed esplicitando rispetto a \sum_{k=1}^n q^{k-1}
otteniamo un’altra espressione del generico numero repunit:
\sum_{k=1}^n q^{k-1}=\frac {q^{n}-1} {q-1}
Sostituendo la sommatoria o la frazione nella 3.2 risultano le espressioni equivalenti:
S_n^A q^{n-1}+S_{n-1}^D={\frac {q^n-1} {q-1}} \sum_{k=1}^n q^{k-1} =\lbrack{{\frac {q^n-1} {q-1}}}\rbrack^2=\lbrack{ \sum_{k=1}^n q^{k-1}}\rbrack^2 3.4
Scambiando i membri otteniamo l’espressione che ci permette di costruire la piramide numerica:
\lbrack{{\frac {q^n-1} {q-1}}}\rbrack \cdot \lbrack{{\frac {q^n-1} {q-1}}}\rbrack=S_n^A q^{n-1}+S_{n-1}^D
\lbrack{{\frac {q^n-1} {q-1}}}\rbrack \cdot \lbrack{{\frac {q^n-1} {q-1}}}\rbrack=q^{n-1} \displaystyle\sum_{k=1}^n kq^{n-k}+\displaystyle\sum_{k=1}^{n-1} kq^{k-1} 3.5
\lbrack{ \displaystyle\sum_{k=1}^n q^{k-1}}\rbrack \cdot \lbrack{ \displaystyle\sum_{k=1}^n q^{k-1}}\rbrack=q^{n-1} \displaystyle\sum_{k=1}^n kq^{n-k}+\displaystyle\sum_{k=1}^{n-1} kq^{k-1}
I numeri repunit \sum_{k=1}^n q^{k-1}=\frac {q^{n}-1} {q-1}, per qualsiasi base q, rappresentano numeri con n cifre tutte uguali a 1; un esempio per n=8 sarà: 11111111 oppure con la frazione \frac {10^{8}-1} {9}=\frac {99999999} {9} = 11111111 .
Prendiamo la base q=10 e per n i valori compresi tra 1 e 9, la 3.5 diviene:
\lbrack{{\frac {10^n-1} {9}}}\rbrack \cdot \lbrack{{\frac {10^n-1} {9}}}\rbrack=10^{n-1} \displaystyle\sum_{k=1}^n k10^{n-k}+\displaystyle\sum_{k=1}^{n-1} k10^{k-1}
e permette di scrivere:

Come secondo esempio prendiamo la base numerica q=16 e per “n” i rispettivi 15 valori: 1,2,3,4,5,6,7,8,9,A,B,C,D,E,F dove per i numeri naturali >9 si sono presi come simboli le prime lettere dell’alfabeto, come si conviene per la base esadecimale. Dalla 3.5 otteniamo:
\lbrack{{\frac {16^n-1} {15}}}\rbrack \cdot \lbrack{{\frac {16^n-1} {15}}}\rbrack=16^{n-1} \displaystyle\sum_{k=1}^n k16^{n-k}+\displaystyle\sum_{k=1}^{n-1} k10^{k-1} ossia in esadecimale:
\lbrack{{\frac {10^n-1} {F}}}\rbrack \cdot \lbrack{{\frac {10^n-1} {F}}}\rbrack=10^{n-1} \displaystyle\sum_{k=1}^n k10^{n-k}+\displaystyle\sum_{k=1}^{n-1} k10^{k-1}, otteniamo:

Albignasego, 07/03/2018